Université d'Angers	Epreuve de Mécanique des Fluides Contrôle Continu Mardi 21 novembre 2000	Année 2000-2001
		Durée : 2h30
Licence de Physique et Applications		S. Chaussedent

La calculatrice et le formulaire sont autorisés

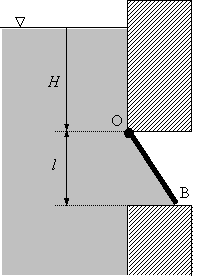
Problème 1 : Vanne a Régulation de Niveaux (barème indicatif : 9 pts)

Une vanne rectangulaire de largeur unité (Dy = 1), de longueur OB = d et de masse m, peut pivoter autour de l’axe Oy et permet de retenir le liquide d’un réservoir. La hauteur H de liquide est repérée par rapport à l’axe Oy. l est la hauteur de l’ouverture pratiquée dans la paroi du réservoir dans laquelle repose la vanne (voir figure 1). On supposera négligeable l’épaisseur de la vanne, et son centre de masse G situé au milieu de OB. Le liquide sera supposé incompressible et de masse volumique r.

1. Calculer la force de pression hydrostatique s’exerçant sur la vanne.

2. Déterminer le point d’application A de cette force .

3. Calculer le moment de la force par rapport à l’axe de pivotement, ainsi que celui du poids de la vanne, également par rapport à l’axe de pivotement.

4. En déduire la hauteur H de liquide à partir de laquelle la vanne s’ouvre automatiquement (exprimer H en fonction de m, d, l et r).

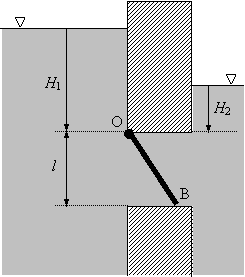
5. On souhaite utiliser cette même vanne pour séparer deux réservoirs contenant les hauteurs H₁ et H₂ d’un même liquide de masse volumique r (voir figure 2). Déterminer les forces et qu’exercent respectivement le liquide du réservoir 1 et celui du réservoir 2 sur la vanne. Après avoir déterminé les points d’application A₁ et A₂ de et , en suivant la même démarche que précédemment, exprimer la différence de niveau DH = H₁-H₂ que cette vanne permet de maintenir constante.

- figure 1 -

- figure 2 -

Problème 2 : Ecoulement autour d’un Mât (barème indicatif : 7 pts)

On souhaite modéliser et caractériser l’écoulement de l’air autour d’un mât cylindrique. Dans ce but, on considérera l’air comme un fluide incompressible s’écoulant dans un plan perpendiculaire à l’axe du mât. Dans ces conditions, on peut décrire l’écoulement à l’aide de la superposition d’un dipôle de potentiel complexe : et d’un écoulement uniforme : Uz, où p et U sont des constantes réelles positives représentant respectivement la vitesse du vent (loin du mât) et le moment dipolaire.

1. Donner la raison pour laquelle il est possible de créer un écoulement résultant de la superposition de ces deux écoulements élémentaires par simple addition de leurs formulations complexes.

2. Après avoir exprimé et développé la forme complexe f(z) de l’écoulement résultant, en déduire la fonction de courant et le potentiel des vitesses.

3. Déterminer le champ de vecteurs vitesse.

4. Montrer qu’il existe deux points d’arrêt et donner leurs coordonnées.

5. Quelles sont les lignes de courant passant par ces points d’arrêt ?

6. Tracer de façon schématique quelques lignes de courant, et plus particulièrement celles passant par les points d’arrêt.

7. Quelle valeur doit-on attribuer au moment dipolaire p pour modéliser l’écoulement d’un vent de vitesse U = 10 m.s^-1 autour d’un mât de rayon R = 20 cm ?

8. Déterminer la vitesse de l’air en contact avec le mât. En quels points celle-ci est-elle maximale ? Que vaut cette vitesse maximale ?

9. Déterminer l’accélération normale et tangentielle de l’air en contact avec le mât. En quels points ces deux composantes sont-elles maximales ?

Problème 3 : Pression de l’Atmosphère (barème indicatif : 4 pts)

On souhaite caractériser la loi de variation de pression de l’atmosphère terrestre en fonction de l’altitude. Pour cela, on considérera l’air comme un gaz parfait vérifiant l’équation d’état : PV = nRT.

1. Montrer que dans ces conditions, la masse volumique est fonction de la pression et s’exprime comme : , où M est la masse molaire du gaz.

2. En supposant que l’atmosphère est adiabatique, on peut montrer que la température est également fonction de la pression et en dépend selon la loi : , où g = 1,4 est le coefficient polytropique de l’air, et a une constante que l’on peut déterminer en considérant qu’à l’altitude z = 0, la pression vaut p₀ pour une température T₀. Poser l’équation fondamentale de la statique des fluides et en déduire la loi de variation de la pression p en fonction de l’altitude z.

3. En déduire qu’il existe une altitude maximale au-delà de laquelle il n’y a plus d’air. Exprimer cette altitude maximale en fonction de g, R, M, de l’accélération de la pesanteur g et de la température T₀ à l’altitude z = 0. Application numérique : R = 8,31 J.K^-1.mol^{-1, M = 30 g.mol-1, g = 9,8 m.s-2} et T₀ = 300 K.

4. Quelle est la loi de variation de la température en fonction de l’altitude ? Quelle température règne-t-il à 10 000 m d’altitude ?