Université d'Angers	Epreuve de Mécanique des Fluides Contrôle Continu Jeudi 13 novembre 2003	Année 2003-2004
		Durée : 2h30
Licence de Physique et Applications		S. Chaussedent

La calculatrice et le formulaire sont autorisés

Problème 1 : Vanne régulatrice de niveau (barème indicatif : 6 pts)

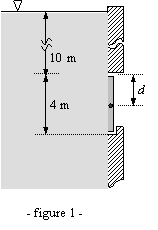
Une porte rectangulaire de 2 m de large est placée dans la paroi verticale d'un réservoir contenant de l'eau (voir figure 1). On souhaite que cette porte s'ouvre automatiquement quand le niveau d'eau par rapport au bord supérieur de la porte dépasse 10 m.

1. Etablir l'expression littérale de la force exercée sur la porte en fonction du niveau d'eau.

2. Localiser le point d’application de cette force.

3. Evaluer numériquement la distance d à laquelle l'axe de rotation de la porte doit être situé pour qu'il y ait ouverture automatique quand le niveau d'eau dépasse 10 m ?

Problème 2 : Cul de bouteille (barème indicatif : 6 pts)

Une bouteille de rayon R contient une hauteur H de liquide (voir figure 2). Le fond est de forme hémisphérique. Déterminer la direction et l'intensité de la résultante des forces de pression qu'exercent le fluide sur les parois de cette bouteille. Comparer ce résultat avec celui qui aurait été obtenu avec une bouteille à fond plat. Conclure.

Problème 3 : Cinématique (barème indicatif : 8 pts)

Dans tout le problème, le fluide pourra être considéré comme parfait et incompressible. Les écoulements seront considérés stationnaires et plans (perpendiculaires à l'axe Oz).

1. Exprimer le potentiel complexe résultant de la superposition d'un écoulement uniforme de la forme et d'un dipôle de la forme , où U et p sont des constantes réelles positives. En déduire la fonction de courant ainsi que le champ de vitesses dans le plan xOy.

2. Déterminer le (ou les) point(s) d'arrêt, et donner l'équation de la ligne de courant passant par ce(s) point(s) d'arrêt. Tracer cette ligne de courant. Expliquer pourquoi, si l'on remplace la surface délimitée par cette ligne de courant par un corps solide, l'écoulement n'est pas modifié. A quel système concret peut correspondre cette modélisation ?

3. Soit le moment dipolaire du dipôle modélisant la présence d'un cylindre de hauteur h, de rayon R, dont l'axe de symétrie est Oz, placé au sein d'un écoulement uniforme de vitesse . On se propose d'étudier l'écoulement résultant lorsque ce cylindre est en rotation à la vitesse angulaire autour de son axe de symétrie. La rotation de ce cylindre peut se modéliser au moyen d'un vortex de circulation . Exprimer la vitesse générée par ce vortex à la distance R de l'origine. En déduire l'expression de en fonction de R et .

4. Pour étudier l'écoulement du vent autour d'un mât de hauteur h, de rayon R, en rotation à la vitesse angulaire , on superpose les écoulements précédents : l'écoulement uniforme de vitesse modélisant le vent, le dipôle de moment p modélisant le mât, et le vortex de circulation modélisant sa rotation. Exprimer le potentiel complexe total en fonction de U, R et w.

5. Calculer la vitesse en tout point de la surface du mât. En déduire que le cercle centré à l'origine et de rayon R constitue une ligne de courant. A quelles conditions portant sur w existe-t-il un (ou des) point(s) d'arrêt à la surface du mât ?

6. On règle la vitesse de rotation du cylindre de sorte à avoir . Dans ces conditions, localiser les deux points d’arrêt à la surface du mât. Quelles sont les accélérations normale et tangentielle en ces deux points ?