Université d'Angers	Epreuve de Mécanique des Fluides Contrôle Continu Jeudi 25 novembre 1999	Année 1999-2000
		Durée : 2h30
Licence de Physique et Applications		S. Chaussedent

Les calculatrices et les formulaires sont autorisés

Problème 1 : Dimensionnement d'un Barrage Poids (barème indicatif : 8 pts)

On considère un barrage de forme parallélépipèdique, de masse volumique r_b, de hauteur H, de largeur l, et de longueur L. De part et d'autre de ce barrage se trouve de l'eau de masse volumique r, avec des hauteurs h₁ et h₂ (voir figure 1).

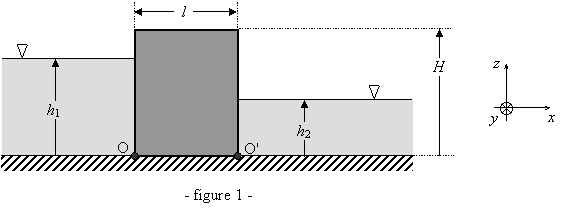
1. Ecrire l'équation fondamentale de la statique des fluides. En déduire la relation liant pression et profondeur pour un fluide incompressible. On considérera l'eau incompressible dans tout le problème.

2. Expliquer qualitativement pourquoi il est possible de ne pas tenir compte de la pression atmosphérique dans le calcul des forces de pression s'exerçant sur le barrage.

3. Calculer les forces de pression et s'exerçant sur les parois du barrage respectivement dues à l'eau se trouvant à gauche et à droite de celui-ci.

4. Trouver la position des points d'applications de chacune de ces deux forces.

5. Soit le poids du barrage. Exprimer et donner la position de son point d'application.

6. Le barrage est maintenu en équilibre sous la seule action de son propre poids : il n'est pas fixé au sol. Calculer, par rapport au point O', le moment des forces , et .

7. Définir la condition pour qu'il y ait risque de basculement du barrage, c'est-à-dire rotation autour de l'arête O'.

8. Dans quelles conditions extrêmes, portant sur les valeurs de h₁ et h₂ , peut-on avoir ce basculement ? En déduire la valeur minimale de l, exprimée en fonction de r, r_b, et H, pour qu'il ne puisse jamais y avoir basculement du barrage quelles que soient les valeurs de h₁ et h₂. Application numérique : r = 10³ kg.m^-3 et r_b= 2.10³ kg.m^-3.

TSVP

Problème 2 : Vortex Double (barème indicatif : 12 pts)

Partie A

1. Soit le potentiel complexe où C est une constante réelle positive. Exprimer la fonction de courant y et le potentiel des vitesses j de cet écoulement.

2. En déduire l'équation des lignes de courant et des équipotentielles. En tracer quelques unes et caractériser cet écoulement.

3. Déterminer le champ de vitesses

4. Calculer la circulation G le long d'une ligne de courant quelconque. Exprimer la constante C en fonction de la circulation G.

5. Cet écoulement est-il rotationnel ?

Partie B

On superpose deux vortex, l'un de circulation G centré en x=a, l'autre de circulation -G centré en x=-a.

1. Donner le potentiel complexe de l'écoulement résultant.

2. On fait tendre la distance a vers zéro. En effectuant un développement limité au premier ordre, réexprimer le potentiel complexe de l'écoulement. On posera 2aG=p.

3. En déduire la fonction de courant y et le potentiel des vitesses j.

4. Montrer que les lignes de courant ont pour équation : où b est une constante réelle. Quelle allure ont ces lignes de courant ? Quel point du plan complexe ont-elles toutes en commun ?

5. Tracer quelques lignes de courant, et (sans calculs) quelques équipotentielles. Comparer cet écoulement avec celui généré par un dipôle.

Partie C

1. Exprimer le potentiel complexe d'un écoulement uniforme de vitesse .

2. On superpose cet écoulement uniforme à l'écoulement de la Partie B. Ecrire le potentiel complexe résultant et exprimer sa fonction de courant y et le potentiel des vitesses j.

3. En déduire le champ de vitesses ainsi que les coordonnées des éventuels points d'arrêt.

4. Déterminer l'équation et l'allure de la ligne de courant passant par ces points d'arrêt.

5. Que se passerait-il si l'on remplaçait la surface délimitée par cette ligne de courant particulière par un corps solide ? Pourquoi ? Quel type d'écoulement réel peut simuler ce potentiel complexe ?