Université d'Angers	Epreuve de Mécanique des Fluides Examen 2^e Session Jeudi 4 septembre 2003	Année 2002-2003
		Durée : 2h30
Licence de Physique et Applications		S. Chaussedent

La calculatrice et le formulaire sont autorisés

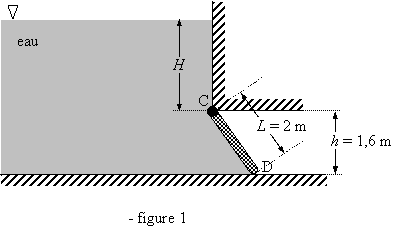
Problème 1 : Vanne Poids (barème indicatif : 7 pts)

La porte rectangulaire CD de la figure 1 a pour longueur L = 2 m et largeur l = 1,8 m (suivant la perpendiculaire au plan de la figure). Son épaisseur étant négligeable, on donne la masse surfacique du matériau homogène la constituant : s = 5110 kg.m^-2. Cette porte a la possibilité de pivoter autour de l'axe C. Le problème que l'on se propose de résoudre consiste à déterminer la hauteur d'eau H à partir de laquelle la porte s'ouvre pour laisser l'eau s'écouler.

1. Déterminer, en intensité et en direction, la force de pression hydrostatique s'exerçant sur la porte.

2. Déterminer la position du point d'application de cette force.

3.

Calculer, d'une part le moment de la force hydrostatique par rapport à l'axe de rotation, et d'autre part le moment du poids de la porte par rapport à l'axe de rotation. En déduire la hauteur d'eau H nécessaire pour qu'il y ait ouverture automatique de la porte.

Problème 2 : Voile de Flettner (barème indicatif : 9 pts)

Dans tout le problème, l'air pourra être considéré comme un fluide parfait incompressible. Les écoulements seront considérés stationnaires et plans (perpendiculaires à l'axe Oz).

1. Exprimer le potentiel complexe résultant de la superposition d'un écoulement uniforme de vitesse , et d'un dipôle de moment dipolaire p>0 centré à l'origine. En déduire la fonction de courant ainsi que le champ de vitesses dans le plan xOy.

2. Déterminer le (ou les) point(s) d'arrêt, et donner l'équation de la ligne de courant passant par ce(s) point(s) d'arrêt. Tracer cette ligne de courant. Expliquer pourquoi, si l'on remplace la surface délimitée par cette ligne de courant par un corps solide, l'écoulement n'est pas modifié. A quel système concret peut correspondre cette modélisation ?

3. Soit le moment dipolaire du dipôle modélisant la présence d'un cylindre de hauteur h, de rayon R, dont l'axe de symétrie est Oz, placé au sein d'un écoulement uniforme de vitesse . On se propose d'étudier l'écoulement résultant lorsque ce cylindre est en rotation à la vitesse angulaire autour de son axe de symétrie. La rotation de ce cylindre peut se modéliser au moyen d'un vortex de circulation . Exprimer la vitesse générée par ce vortex à la distance R de l'origine. En déduire l'expression de en fonction de R et .

4. Pour étudier l'écoulement du vent autour d'un mât de hauteur h, de rayon R, en rotation à la vitesse angulaire , on superpose les écoulements précédents : l'écoulement uniforme de vitesse modélisant le vent, le dipôle de moment p modélisant le mât, et le vortex de circulation modélisant sa rotation. Exprimer le potentiel complexe total en fonction de U, R et w.

5. Calculer la vitesse en tout point de la surface du mât. En déduire que le cercle centré à l'origine et de rayon R constitue une ligne de courant. A quelles conditions portant sur w existe-t-il un (ou des) point(s) d'arrêt à la surface du mât ?

6. En appliquant l'équation de Bernoulli entre un point situé loin du mât (où la pression vaut p₀ et la vitesse U) et un point d'arrêt sur la surface du mât, déterminer la pression au point d'arrêt. Toujours en appliquant l'équation de Bernoulli, en déduire la pression en tout point de la surface du mât.

7. Calculer la résultantedes forces de pression s'exerçant sur le mât de hauteur h. On donnera l'expression de sa composante F_x suivant x, et de sa composante F_y suivant y. Commenter le résultat obtenu pour F_x et déterminer la valeur de w donnant une force propulsive maximale dans la direction des y croissants.

Problème 3 : Similitudes (barème indicatif : 4 pts)

On souhaite étudier le couple C nécessaire pour faire tourner un disque de diamètre D, à la vitesse angulaire w, dans un fluide de masse volumique r et de viscosité m.

1. Etablir l’analyse dimensionnelle du phénomène et donner l’expression des deux produits P sans dimensions qui interviennent dans cette étude (on choisira comme grandeurs primaires D, w et r).

2. Un disque de 22,5 cm de diamètre tournant à 1400 tr/min dans l’eau (m_eau = 10^-3 kg.m^-1.s^-1 et r_eau = 10³ kg.m^-3) nécessite un couple d’entraînement de 1,1 N.m. On veut prévoir le fonctionnement d’un disque semblable, de 67,5 cm de diamètre, tournant dans l’air (m_air = 1,7.10^-5 kg.m^-1.s^-1 et r_air = 1,225 kg.m^-3).

a) A quelle vitesse doit-on faire tourner ce disque dans l’air pour qu’il y ait similitude avec celui tournant dans l’eau ?

b) Dans ces conditions, quels sont le couple et la puissance nécessaires à son entraînement ?