Université d'Angers	Epreuve de Mécanique des Fluides Examen 1^ère Session Vendredi 9 février 2001	Année 2000-2001
		Durée : 2h30
Licence de Physique et Applications		S. Chaussedent

La calculatrice et le formulaire sont autorisés

Problème 1 : Similitudes & Turbulences (barème indicatif : 6 pts)

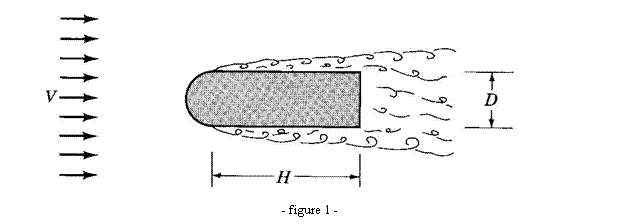
Une structure métallique intégrant l’architecture d’un pont présente la forme donnée par la vue en coupe de la figure 1. On sait que lorsqu’un écoulement stationnaire d’air rencontre ce type d’objet, des turbulences sont créées en aval. Ces tourbillons, de fréquence caractéristique w, sont responsables de forces agissant de manière néfaste sur la structure du pont, c’est pourquoi il convient de les appréhender en effectuant des mesures sur un modèle réduit avant de construire le prototype.

Pour le prototype, on a D = 0,1 m, H = 0,3 m et le vent qu’il faudra considérer est de vitesse V = 50 km.h^-1. On réalise alors une maquette telle que D_m = 20 mm que l’on place dans un tunnel à eau. On y mesure une fréquence des turbulences w_m = 49,5 Hz.

1. Etablir la liste des grandeurs caractéristiques permettant de décrire le problème. A combien de produits sans dimensions P peut être ramenée l’étude ?

2. Déterminer et nommer chacun de ces produits P.

3. Sachant que la similitude géométrique est respectée, calculer H_m.

4. A quelle vitesse V_m doit s’écouler l’eau autour de la maquette pour pouvoir transposer la mesure de w_m sur la maquette à celle que l’on obtiendra sur le prototype ?

5. En déduire la valeur de la fréquence caractéristique des turbulences auxquelles sera soumise la structure métallique prototype ?

A.N. : m_air = 1,79.10^{-5 kg.m-1}.s^-1 ; m_eau = 10^{-3 kg.m-1}.s^-1 ; r_air = 1,23 kg.m^-3 ; r_eau = 10³ kg.m^-3.

Problème 2 : Ecoulement entre 2 plaques inclinées (barème indicatif : 9 pts)

On considère l’écoulement stationnaire et laminaire d’un fluide visqueux (viscosité m) et incompressible (masse volumique r) entre deux plaques infinies parallèles et inclinées d’un angle a avec l’horizontale.

La plaque supérieure est animée d’une vitesse constante U alors que la plaque inférieure reste fixe. On choisira comme repère cartésien celui représenté sur la figure 2.

1. A partir de l’équation de continuité et de la symétrie du problème, établir que la vitesse du fluide s’exprime comme : .

2. Projeter l’équation de Navier-Stokes sur les trois axes du repère cartésien.

3. Négliger le poids de la plaque supérieure revient à poser constante et égale à p₀ la pression en z =H. Que peut-on en déduire sur le gradient de pression suivant l’axe x ? Déterminer l’expression de la pression p(z).

4. Montrer que le profil de vitesse est de la forme u(z) = A z² + B z + C. Etablir les conditions aux limites permettant de trouver les trois constantes A, B et C.

5. Exprimer le débit volumique de liquide s’écoulant entre les deux plaques, sur une épaisseur unitaire (Dy = 1), en fonction de r, m, g, a, H et U. Quelle condition portant sur U permet d’assurer un débit positif, et par voie de conséquence l’ascension globale du liquide ?

6. En se plaçant dans le cas limite d’un débit nul, donner les éléments du tenseur des contraintes s’exerçant sur le fluide au contact de la plaque supérieure. En déduire la force de frottement qu’exerce le liquide sur cette plaque (considérer la force par unité de longueur suivant x et suivant y). Quelle puissance (par unité de surface) doit-on développer pour tirer la plaque ?

7. Qu’advient-il de ce problème en l’absence de plaque supérieure ? En quoi les conditions aux limites sont-elles modifiées ? Exprimer dans ces conditions le nouveau débit volumique et déterminer la force de frottement par unité de surface qu’exerce l’écoulement du liquide sur la plaque inférieure.

Problème 3 : Conduite Gravitaire (barème indicatif : 5 pts)

Une conduite amène l’eau (supposée incompressible, de masse volumique r ) d’un barrage vers une turbine (voir figure 3). La conduite cylindrique, de diamètre constant D = 30 cm, se termine horizontalement, son axe étant situé à H = 160 m au dessous de la surface libre de l’eau dans le barrage de grande capacité. Le départ de la conduite est à H₀ = 20 m au dessous de la surface libre de l’eau, de niveau pratiquement constant. On négligera tout frottement (et donc les pertes de charge). Pour les applications numériques, on prendra : la pression atmosphérique P₀ = 10⁵ Pa, l'accélération de la pesanteur g = 10 m.s^-2 et r = 10³ kg.m^-3.

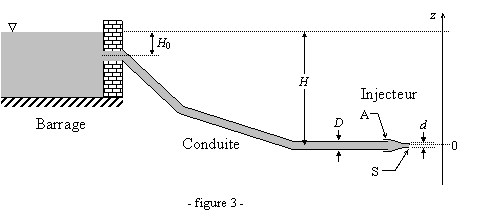
1. Calculer la vitesse de l’eau à la sortie A de la conduite (sans injecteur).

2. Montrer que l’on a un phénomène de cavitation dans une région de la conduite que l’on déterminera (on supposera que la cavitation apparaît quand la pression devient voisine de zéro).

3. On visse sur l’extrémité A un injecteur de diamètre de sortie d et d’axe horizontal. Montrer que la cavitation disparaît totalement pour d<d₀ ; calculer d₀.

4. En prenant d = 15 cm, calculer la vitesse V_i de l’eau à la sortie S, le débit volumique q_v ainsi que la puissance cinétique du jet (P = pression cinétique x débit volumique).