Université d'Angers	Epreuve de Mécanique des Fluides Examen 1^re Session Jeudi 22 janvier 2004	Année 2003-2004
		Durée : 2h30
Licence de Physique et Applications		S. Chaussedent

La calculatrice et le formulaire sont autorisés

Problème 1 : Viscosimètre (barème indicatif : 7 pts)

On considère une conduite cylindrique de rayon R, disposée verticalement et dans laquelle s’écoule de haut en bas un liquide newtonien incompressible de masse volumique r et de viscosité dynamique m. On supposera que la pression à l’entrée est identique à celle en sortie (l’écoulement est donc assuré par la gravité). L’écoulement sera considéré stationnaire et laminaire.

1. Compte tenu de la géométrie de l’écoulement et en posant l’équation de continuité, montrer que .

2. Etablir et projeter l’équation de Navier-Stokes dans le repère cylindrique de la conduite. En déduire que la pression est uniforme dans toute la conduite et donner une expression analytique du profil de vitesse w(r) qui tienne compte des conditions aux limites.

3. Exprimer le débit volumique ainsi que la vitesse moyenne de l’écoulement.

4. Si l’on dispose d’une conduite de rayon R = 1 mm, quelle viscosité cinématique (n=m/r) minimale doit avoir le fluide pour que l’hypothèse d’un écoulement laminaire soit valide ?

Problème 2 : Similitudes et Maquettes (barème indicatif : 7 pts)

Pour déterminer la puissance d'un navire de longueur L = 100 m, de surface immergée S = 2000 m² et destiné à naviguer en mer à la vitesse de 16 nœuds, on réalise une maquette à l'échelle 1/25 que l'on essaie dans un bassin d'eau douce. On admet que la traînée d'un corps flottant est la somme de deux forces : celle, F₁, due aux frottements visqueux et celle, F₂, due aux ondes de surface.

On donne 1 nœud = 1,850 km.h^-1. On notera F, V, S,… les grandeurs relatives au navire prototype et F', V', S',… celles relatives à sa maquette.

1. De quelles grandeurs dépendent F₁ et F₂ ?

2. Par analyse dimensionnelle, donner une expression de F₁ et F₂ en faisant apparaître leur dépendance envers les nombres de Reynolds ou de Froude.

On donne et .

Par la suite, on admettra que la traînée due aux frottements s'exprime : , où le coefficient de frottement visqueux est donné par les formules :

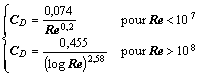
On prendra pour l'eau de mer : r = 1,030.10³ kg.m^-3 et m = 1,2.10^-3 N.s.m^-2 ;

et pour l'eau douce : r' = 1,000.10³ kg.m^-3 et m' = 1,1.10^-3 N.s.m^-2 ;

3. En respectant la similitude de Froude, déterminer la vitesse à donner à la maquette.

4. Déterminer la traînée F'₁ exercée par les frottements sur la maquette.

5. On mesure sur la maquette une force de traînée totale F' = 17 N. En déduire la traînée F'₂ due aux ondes de surface. Calculer la traînée F₂.

6. Calculer la traînée totale F du navire prototype et la puissance nécessaire correspondante.

Problème 3 : Eolienne (barème indicatif : 6 pts)

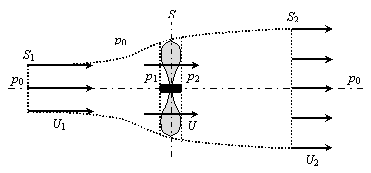
Une éolienne est un dispositif à hélice qui, placé dans un fluide en mouvement, ralentit une fraction de ce fluide en transformant en travail (sur l’arbre de l’hélice) l’énergie cinétique cédée par le fluide.

Pour décrire ce phénomène, on utilise en première approche une théorie unidimensionnelle qui permet de ne pas se préoccuper de l’écoulement complexe autour des pales de l’hélice. On peut ainsi considérer :

Ø que les particules fluides sur lesquelles l’hélice a une action s’écoulent dans un tube de courant qui s’appuie sur le cercle dont l’aire S est balayée par les pales.

Ø que l’écoulement est permanent et globalement unidimensionnel : les vitesses sont uniformes dans chacune des sections du tube de courant et en particulier dans S₁, section amont où la vitesse est U₁, dans S, section de l’hélice où la vitesse est U, et dans S₂, section aval où la vitesse est U₂ (U₁>U>U₂).

Ø que le fluide est parfait, incompressible (de masse volumique r) et non pesant.

Ø que le long de la frontière du tube et dans les sections S₁ et S₂ la pression est celle de l’atmosphère (p₀).

1. Exprimer la chute de pression Dp=p₁-p₂ à la traversée de l’hélice.

2. En déduire une expression de la force R exercée par le fluide sur l’hélice en fonction de U₁ et U₂.

3. Par application du théorème d’Euler, exprimer cette même force R en fonction de U, U₁ et U₂.

4. En identifiant ces deux expressions de R, en déduire une relation entre U, U₁ et U₂.

5. En posant U₂=aU₁, avec 0<a<1, exprimer en fonction de a et U₁ la puissance P recueillie par l’hélice.

6. On définit le rendement h d’une éolienne par le rapport de puissance P recueillie à la puissance totale disponible dans un tube de courant de section S où la vitesse du vent est U₁. Exprimer h. Pour quelle valeur de a le rendement est maximum ? Que vaut alors ce rendement h_max ?

7. En pratique, le rendement le plus élevé que l’on puisse obtenir est de l’ordre de 0,5. Comment peut-on expliquer cet écart ? Calculer, pour h_max =0,5, la puissance maximale disponible sur l’arbre d’une éolienne de 30 m de diamètre soumise à un vent de 20 m.s^-1 (on prendra r_air = 1,25 kg.m^-3).