Université d'Angers	Epreuve de Mécanique des Fluides U.E. S6-PC2 Examen 1^re session Vendredi 27 mai 2005	Année 2004-2005
Licence mention Physique-Chimie		S. Chaussedent

La calculatrice et le formulaire sont autorisés

Problème 1 : Ecoulement Laminaire (barème indicatif : 7 pts)

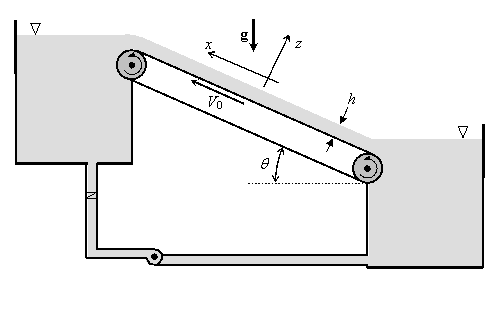
Afin d’obtenir des écoulements laminaires en laboratoire, on réalise le montage ci-dessus. Une couche d’épaisseur h d’un liquide incompressible de masse volumique r et de viscosité m est déposée sur un tapis roulant animé d’une vitesse V₀ et incliné d’un angle q par rapport à l’horizontal. On supposera l’écoulement du liquide sur le tapis roulant stationnaire et laminaire.

1. Compte tenu de la géométrie de la couche et en posant l’équation de continuité, montrer que .

2. Projeter l’équation de Navier-Stokes sur les axes x et z (prendre garde à l’orientation de la gravité !). En remarquant que la pression à l’interface liquide-atmosphère est constante, montrer que le gradient de pression est non nul seulement suivant z. Donner alors l’expression de p(z).

3. Déterminer le profil de vitesse de la couche en utilisant les conditions aux limites (on remarquera que la contrainte tangentielle à la surface libre est nulle).

4. Calculer le débit de liquide à travers l’épaisseur h, pour une largeur unité du tapis roulant.

5. A quelle vitesse V₀ doit avancer le tapis pour que ce débit soit nul ?

6. Après avoir exprimé la contrainte exercée par le tapis sur le fluide, trouver la force de frottement totale exercée par le fluide sur la longueur L du tapis. A quelle autre force cette force de frottement peut-elle être identifiée ? Donner l’expression de la puissance nécessaire pour entraîner le tapis roulant.

Problème 2 : Ecoulement autour d’un Mât (barème indicatif : 7 pts)

On souhaite modéliser et caractériser l’écoulement de l’air autour d’un mât cylindrique. Dans ce but, on considérera l’air comme un fluide incompressible s’écoulant dans un plan perpendiculaire à l’axe du mât. Dans ces conditions, on peut décrire l’écoulement à l’aide de la superposition d’un dipôle de potentiel complexe : et d’un écoulement uniforme : Uz, où p et U sont des constantes réelles positives représentant respectivement la vitesse du vent (loin du mât) et le moment dipolaire.

1. Après avoir exprimé et développé la forme complexe f(z) de l’écoulement résultant, en déduire la fonction de courant et le potentiel des vitesses.

2. Déterminer le champ de vecteurs vitesse.

3. Montrer qu’il existe deux points d’arrêt et donner leurs coordonnées.

4. Quelles sont les lignes de courant passant par ces points d’arrêt ?

5. Tracer de façon schématique quelques lignes de courant, et plus particulièrement celles passant par les points d’arrêt.

6. Quelle valeur doit-on attribuer au moment dipolaire p pour modéliser l’écoulement d’un vent de vitesse U = 10 m.s^-1 autour d’un mât de rayon R = 20 cm ?

7. Déterminer l’expression de la vitesse de l’air en contact avec le mât. En quels points celle-ci est-elle maximale ? Que vaut cette vitesse maximale ?

8. En supposant que loin en amont du mât la pression vaut p₀, appliquer l’équation de Bernoulli pour déterminer l’expression de la pression en tout point de la surface du mât. En quels points est-elle maximale et minimale ? Imaginer et décrire une méthode qui permettrait la mesure de la vitesse du vent.