1. Hydrostatique

———— Ex. 1.1 ——————————————————————————

Formuler l'équation fondamentale de la statique des fluides dans le cas où le fluide est uniformément accéléré. Appliquer ce résultat au cas d'un tube en U partiellement rempli d'un liquide et subissant une accélération uniforme horizontale (voir figure 1.1). Les deux branches du U étant distantes de l, trouver ainsi la différence de niveau h due à cette accélération.

———— Ex. 1.2 ——————————————————————————

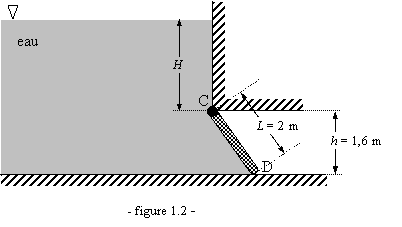
La porte rectangulaire CD de la figure 1.2 a pour longueur L = 2 m et largeur l = 1,8 m (suivant la perpendiculaire au plan de la figure). Son épaisseur étant négligeable, on donne la masse surfacique du matériau homogène la constituant : s = 5110 kg.m^-2. Cette porte a la possibilité de pivoter autour de l'axe C. On se propose de déterminer la hauteur d'eau H à partir de laquelle la porte s'ouvre pour laisser l'eau s'écouler.

1. Déterminer la force de pression hydrostatique s'exerçant sur la porte.

2. Déterminer la position du point d'application de cette force.

3. Calculer, d'une part le moment de la force hydrostatique par rapport à l'axe de rotation, et d'autre part le moment du poids de la porte par rapport à l'axe de rotation. En déduire la hauteur d'eau H nécessaire pour qu'il y ait ouverture automatique de la porte.

———— Ex. 1.3 ——————————————————————————

La masse volumique de la digue représentée sur la figure 1.3 est de 2360 kg.m^-3. Déterminer le coefficient de friction minimal requis entre la digue et ses fondations pour qu'il y ait absence de glissement. (effectuer l'analyse pour une unité de longueur de la digue).

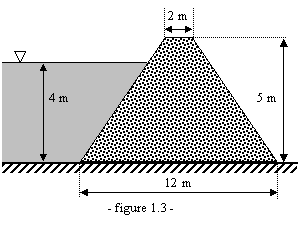
———— Ex. 1.4 ——————————————————————————

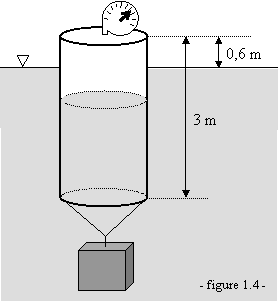
Un réservoir de 1 m de diamètre et de masse 90 kg est clos à son extrémité supérieure. L'autre extrémité est ouverte et descendue dans l'eau à l'aide d'un bloc d'acier de masse volumique 7840 kg.m^-3 (voir figure 1.4). On suppose que l'air emprisonné dans le réservoir est comprimé à température constante. Déterminer :

1. la lecture d'un manomètre donnant la pression dans le réservoir ;

2. le volume du bloc d'acier.

———— Ex. 1.5 ——————————————————————————

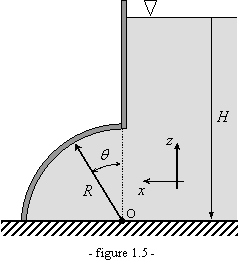
On cherche à caractériser la force de pression hydrostatique s’exerçant sur l’arc circulaire de la figure 1.5. On raisonnera sur une largeur unité.

1. Exprimer la pression hydrostatique en tout point de l’arc en fonction de H, R, r, g et q.

2. En déduire les deux composantes dF_x et dF_z de la force de pression élémentaire en chaque point de l’arc.

3. Exprimer les deux résultantes F_x et F_z en fonction de H, R, r et g.

4. Si on note A le point de l’arc où s’applique la force, montrer que le moment de cette force par rapport au point O est nul. En déduire, en fonction de H et R, l’expression de l’angle q_A repérant la position de A.

5. Quelles valeurs limites peut prendre l’angle q_A en fonction des variations de H ?

———— Ex. 1.6 ——————————————————————————

En tenant compte de la compressibilité de l’air atmosphérique, et en supposant que la température de l’atmosphère obéit à la loi T(z) = T₀ – B.z, déterminer la limite d’altitude de l’atmosphère selon ce modèle. On prendra T₀ = 293 K comme température au niveau du sol, et B = 7,5 K.km^-1.