2. Cinématique

———— Ex. 2.1 ——————————————————————————

1. Ecrire l'équation de continuité en symétrie sphérique pour l'écoulement stationnaire et conservatif d'un fluide incompressible. En déduire l'expression de la vitesse en un point quelconque lorsque cet écoulement est radial, dirigé vers l'origine.

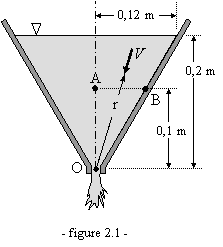
2. On suppose que de l'eau coule en régime permanent à travers l'entonnoir représenté sur la figure 2.1. L'écoulement étant considéré comme radial, centré en O, l'expression de la vitesse est celle établie dans la question précédente. Déterminer l'accélération aux points A et B sachant que la vitesse en A est de 0,6 m.s^-1.

———— Ex. 2.2 ——————————————————————————

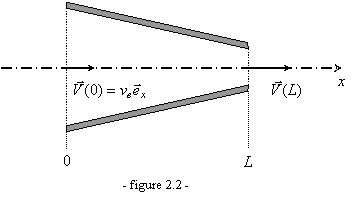
On considère l'écoulement stationnaire et unidimensionnel d'un fluide incompressible à l'intérieur de la buse représentée figure 2.2. La vitesse du fluide le long de l'axe est donnée par :

où est la vitesse à l'entrée de la buse et sa longueur.

1. Déterminer l'accélération d'une particule fluide traversant la buse le long de l'axe.

2. Déterminer, en fonction du temps, la position d'une particule initialement située à l'entrée de la buse. En déduire son accélération.

3. Les deux accélérations calculées sont-elles différentes ? Pourquoi ?

———— Ex. 2.3 ——————————————————————————

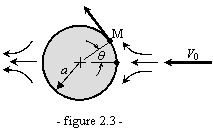
Un modèle d’écoulement stationnaire autour d’un cylindre (voir figure 2.3) a permis de formuler l’expression de la vitesse du fluide en tout point M de la surface :

.

Déterminer l’accélération normale et tangentielle en fonction de a, q et V₀.

———— Ex. 2.4 ——————————————————————————

L'écoulement d'eau à travers les orifices de la rampe d'arrosage représentée figure 2.4 génère un champ de vecteurs vitesse tel que , où , et sont des constantes. Ainsi, la composante de la vitesse selon l'axe y reste constante : et celle selon l'axe x coïncide, en , avec la vitesse de déplacement de la rampe d'arrosage : .

1. Déterminer la ligne de courant passant par l'origine à ; à .

2. Déterminer la trajectoire de la particule émise à l'origine à ; à .

3. Déterminer l'allure de la ligne d'émission relative à l'origine, à un instant t quelconque.

———— Ex. 2.5 ——————————————————————————

La fonction de courant de l'écoulement plan d'un fluide incompressible est donnée par l'équation :

,

où est en m³.s^-1 et x, y sont en m.

1. Tracer la(les) ligne(s) de courant passant par l'origine.

2. Déterminer le débit volumique à travers le segment AB de la figure 2.5.

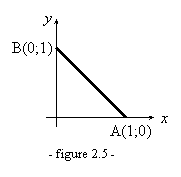
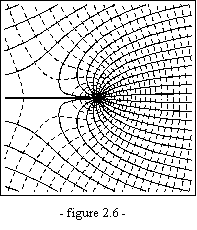
———— Ex. 2.6 ——————————————————————————

L'écoulement plan de la figure 2.6 correspond au potentiel des vitesses suivant :

,

où A et B sont deux constantes réelles positives. Déterminer la fonction de courant associée et localiser d'éventuels points d'arrêt. Caractériser qualitativement cet écoulement en s'aidant de la représentation qui en est donnée.

———— Ex. 2.7 ——————————————————————————

On considère la superposition d'un écoulement uniforme dans la direction des x croissants, avec un vortex centré sur l'origine. En supposant que la ligne de courant passe par le point de coordonnées (2;0), déterminer son équation.

———— Ex. 2.8 ——————————————————————————

De l'eau s'écoule sur une surface plane avec une vitesse uniforme de 1,5 m.s^-1 (voir la figure 2.8). Une pompe aspire l'eau à travers une fente placée dans la surface plane, avec un débit volumique de 4 l.s^-1 par unité de largeur de fente. En supposant l'eau incompressible, l'écoulement peut être modélisé par la superposition d'un écoulement uniforme et d'un puits.

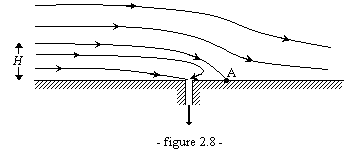
1. Localiser l'endroit où la vitesse de l'eau est nulle et déterminer l'équation de la ligne de courant passant par ce point.

2. A quelle hauteur H par rapport à la surface doit se situer une particule fluide pour ne pas être aspirée par la pompe ?

———— Ex. 2.9 ——————————————————————————

On peut modéliser l'écoulement plan d'un tourbillon par superposition des deux écoulements plans suivants : un puits de débit -q_v<0 situé à l'origine, et un vortex de circulation -G<0 centré sur l'origine.

1. Déterminer le potentiel complexe de l'écoulement résultant. En déduire le potentiel des vitesses et la fonction de courant.

2. Déterminer l'équation d'une ligne de courant. En déduire l'allure des lignes de courant et des équipotentielles.

3. Déterminer le champ de vitesse et vérifier que l'écoulement est irrotationnel. Calculer la circulation du vecteur vitesse sur un cercle centré sur l'origine. Calculer le débit volumique à travers le même cercle. Que peut-on remarquer ? Quelle propriété remarquable présente l'angle () ?

4. Donner les coordonnées et d'une particule se trouvant à et à l'instant . Quel temps met-elle pour atteindre l'origine ?

5. L'écoulement étant irrotationnel, la dynamique des fluides permet de montrer que dans ce cas la pression totale est constante en tout point de l'écoulement, c'est-à-dire , étant la pression hydrostatique, et repérant un plan horizontal dans lequel s'observe l'écoulement plan étudié précédemment. On considère alors un réservoir d'eau d'étendue infinie et de profondeur h (selon l'axe z) qui serait le siège d'un tel tourbillon. Déterminer la pression totale en un point de la surface libre, loin du tourbillon dont l'axe est confondu avec l'axe z. En déduire l'équation de la surface libre en fonction des coordonnées de l'espace (). Schématiser l'allure de cette surface libre.