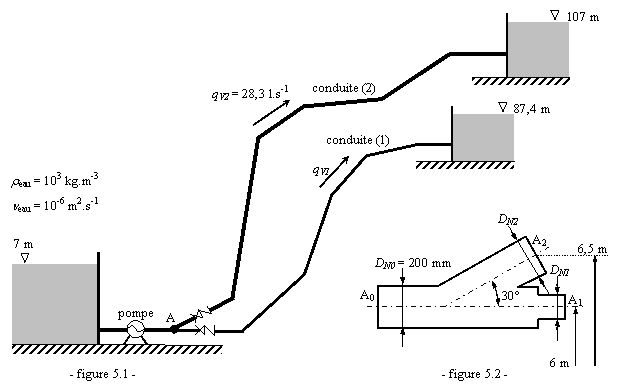![]()

5. Pertes de charge & Bernoulli généralisé
———— Ex.
5.1 ——————————————————————————
Le dispositif suivant vise à
alimenter deux réservoirs, situés en hauteur à deux altitudes différentes, en
utilisant deux conduites connectées à une même pompe qui aspire l'eau dans un réservoir
principal (voir la figure 5.1).
La conduite (1) présente un
diamètre nominal DN1 = 150
mm, une rugosité absolue e1 = 0,09 mm,
une longueur L1 = 1232 m
et transite un débit qV1.
Elle possède une vanne papillon et un clapet anti-retour à battant. En régime
établi, le coefficient de perte de charge dans ce clapet est estimé à KCL1 = 0,17 et la vanne
papillon est totalement ouverte (KV1 = 0,24).
La conduite (2) présente un
diamètre nominal DN2 = 200
mm et une rugosité absolue e2 = 0,15 mm.
Le long du profil en long, la perte de charge due aux singularités est estimée
à 7% de la perte de charge régulière. Elle comporte une vanne à opercule
totalement ouverte (KV2 =
0,07) et un clapet à battant dont le coefficient de perte de charge est KCL2 = 0,23. Sa longueur est L2 = 2450 m et elle transite
un débit qV2 = 28,3 l.s-1.
Les pertes de charge dans le té
des conduites et à l'aspiration de la pompe seront négligées.
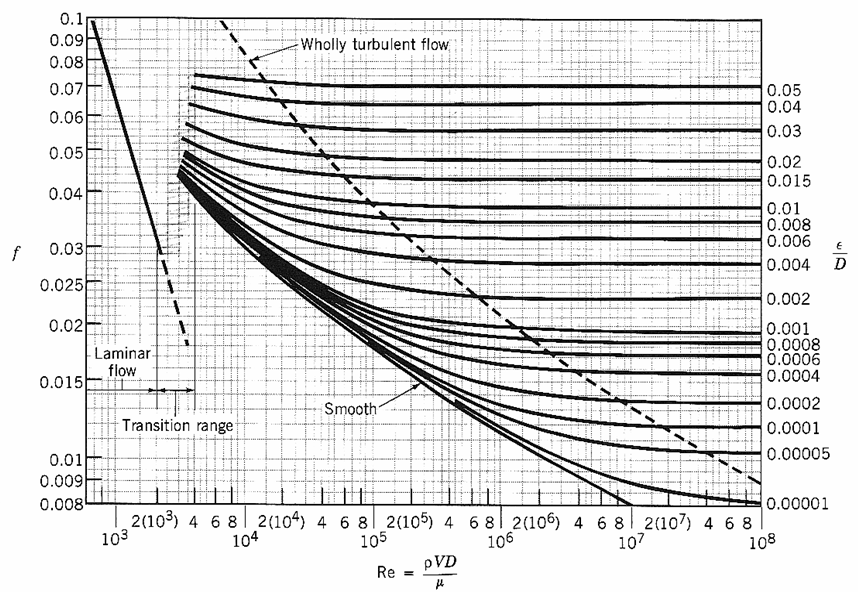
On donne en annexe le diagramme
de Moody
permettant de connaître le coefficient de friction en fonction du nombre de Reynolds et du coefficient de rugosité
relative e /D.
1.
Calculer la charge à la sortie de la pompe.
2.
Si la charge à la sortie de la pompe est de 128 m
d'eau, déterminer le débit qV1
dans la conduite (1). (Pour déterminer la perte de charge régulière dans la
conduite il est nécessaire de connaître la vitesse, donc le débit ; on ne peut
donc résoudre le problème que par approximations successives).
3.
Calculer, en intensité et en direction, l'action
de l'eau sur le té de raccordement A (voir figure 5.2).