Université d'Angers
	DEUG STU2 – ST41 2001-2002	PHYSIQUE - TD 7
	S. Chaussedent	Prismes polariseurs Wollaston & Nicol

Exercice I

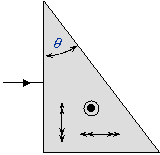On considère un prisme en quartz d'angle q = 30°, éclairé normalement par un faisceau de lumière monochromatique non polarisée. Selon l'orientation de l'axe optique, déterminer l'angle D entre les deux faisceaux transmis en sortie. Pour cela, faire la construction de Huygens pour les trois orientations de l'axe optique proposées ci-contre (on donne n_o = 1,5442 et n_e = 1,5530).

Exercice II

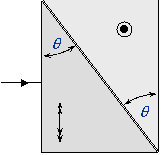
Le système de Wollaston est constitué de deux prismes en quartz accolés comme le montre la figure ci-contre. L'axe optique du premier est parallèle au plan d'entrée. L'axe optique du second est perpendiculaire à celui du premier. L'angle q = 30° est le même pour les deux prismes. Sachant que pour le quartz n_o = 1,5442 et n_e = 1,5530, déterminer la valeur de l'angle D entre les deux faisceaux transmis en sortie du système (utiliser la construction de Huygens).

Exercice III

On considère un rhomboèdre de spath dont le plan de section principale ACA'C' contient l'axe optique ainsi que la normale à la face ABCD.

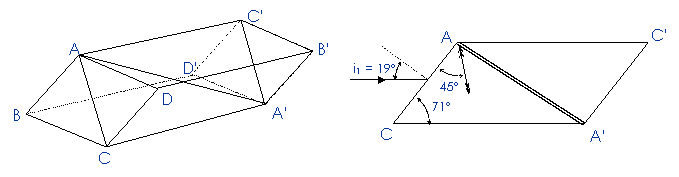
L'axe optique fait un angle de 45° avec AC et l'angle (ACA') est égal à 71°. Le cristal est scié suivant un plan diagonal, perpendiculaire à ACA'C', contenant AA'. On recolle ensuite les deux prismes obtenus avec du baume du Canada dont l'indice de réfraction vaut N = 1,55. On éclaire le prisme avec un angle d'incidence i₁ = 19°. Observe-t-on toujours deux faisceaux émergents ? Pour répondre à cette question, on calculera l'angle d'incidence b du rayon ordinaire sur la face AA'. On donne l'angle (CAA') = 87°, n_o = 1,6584 et n_e = 1,4865.